Journal Name: International Journal of Cancer and Treatment
Article Type: Clinical Trial
Received date: 16 January, 2020
Accepted date: 18 March, 2020
Published date: 25 March, 2020
Citation: Rahman M, Kausar A, Mondol M, Sujan M, Azhari HA, et al. (2020) Analysis of NTCP based Radiobiological Models: A Systematic Review of Literatures. Int J Cancer Treat Vol: 3, Issu: 1 (03-07).
Copyright: © 2020 Rahman M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
To achieve the optimal treatment goal, radiobiological parameters have to evaluate and predict the outcome of this treatment plan in terms of both TCP and NTCP. Different types of radiobiological model were used to achieve prescribed treatment dose of radiation during the tumor control. Where TCP models play an important role in order to achieve desired dose to the tumor. A suitable NTCP model was theoretically found among different models that can be used in treatment plan evaluation. Theoretically, six different radiobiological dose response models were analyzed in this project. Lyman–Kutcher–Burman, Critical element, critical volume, Relative Seriality, Parallel architecture, Weibull distribution models were analyzed from the derivation. All models were discussed elaborately with its various parameters and were used in the calculation of normal tissue complication probability during the treatment in radiotherapy. Further, all models were compared with each other. The models denote the dose for 50% complication probability (D50) parameters is the most commonly used radiobiological models for the normal tissues. The functional subunit response models (critical element & Relative seriality, Critical Volume, parallel architecture) are used in the derivation of the formulae for the normal tissue.
Since all complicated NTCP model predict same as the simple NTCP model that is Lyman–Kutcher–Burman model as well as it is computationally efficient. Also Lyman–Kutcher–Burman model can be used in different treatment planning system incorporating with other model. For this reason, our suggested model is Lyman–Kutcher– Burman NTCP model which can be used in treatment plan evaluation. After analyzing six different model of NTCP, finding of the study is the treatment plan evaluation in where Lyman–Kutcher–Burman model is the best model for biological plan evaluation.
Keywords: Radiobiological Model, TCP, NTCP.
Abstract
To achieve the optimal treatment goal, radiobiological parameters have to evaluate and predict the outcome of this treatment plan in terms of both TCP and NTCP. Different types of radiobiological model were used to achieve prescribed treatment dose of radiation during the tumor control. Where TCP models play an important role in order to achieve desired dose to the tumor. A suitable NTCP model was theoretically found among different models that can be used in treatment plan evaluation. Theoretically, six different radiobiological dose response models were analyzed in this project. Lyman–Kutcher–Burman, Critical element, critical volume, Relative Seriality, Parallel architecture, Weibull distribution models were analyzed from the derivation. All models were discussed elaborately with its various parameters and were used in the calculation of normal tissue complication probability during the treatment in radiotherapy. Further, all models were compared with each other. The models denote the dose for 50% complication probability (D50) parameters is the most commonly used radiobiological models for the normal tissues. The functional subunit response models (critical element & Relative seriality, Critical Volume, parallel architecture) are used in the derivation of the formulae for the normal tissue.
Since all complicated NTCP model predict same as the simple NTCP model that is Lyman–Kutcher–Burman model as well as it is computationally efficient. Also Lyman–Kutcher–Burman model can be used in different treatment planning system incorporating with other model. For this reason, our suggested model is Lyman–Kutcher– Burman NTCP model which can be used in treatment plan evaluation. After analyzing six different model of NTCP, finding of the study is the treatment plan evaluation in where Lyman–Kutcher–Burman model is the best model for biological plan evaluation.
Keywords: Radiobiological Model, TCP, NTCP.
Introduction: Radiobiological models is to predict the radiation response of biological systems While early approaches focused on modeling the radiation response for different fractionation schemes, newer developments attempt to model effect probabilities (TCP and NTCP), their volume dependence and the relative biological efficiency (RBE) of radiation with high linear energy transfer LET [1].
To reduce the suffering and death due to cancer is now one of the biggest challenges ever. Continuous research and technical developments give us hope and confidence about winning the battle against cancer. Radiotherapy has been a major weapon in this battle for a long time. About 60% of cancer patients receive radiotherapy as part of their disease management. The goal of radiation therapy is to deliver a therapeutic dose of radiation to target tissues while minimizing the risks of normal tissue complications. The radiotherapy has been based describe to the best possible tumor control for the case in which all regions of the tumor have exactly the same biological characteristics and sensitivities to radiation [2].
A biologically based model is developed for normal tissue complication probability as a function of dose and irradiated volume fraction for organs. The organ is assumed to be composed of functional subunits which are arranged in a parallel architecture. The complication is produced only if a sufficiently large fraction of the FSUs is inactivated by radiation and an FSU is inactivated only when all the clonogenic cells within it are killed [3].
A model of normal tissue complication probability for tissues that may be represented by critical element architecture. We derive formulas for complication probability that apply to both a partial volume irradiation and to an arbitrary inhomogeneous dose distribution. The dose-volume iso-effect relationship which is a consequence of critical element architecture is discussed and compared to the empirical power law relationship.
A dose-volume histogram reduction scheme for a “pure” critical element model is derived. The existing published dose-volume histogram reduction algorithms are analyzed. The study has shown that the existing algorithms, developed empirically without an explicit biophysical model, have a close relationship to the critical element model at low levels of complication probability [4].
The Empirical models have also found their niche. The Lyman, Kutcher and Burman Model, Relative Seriality Model, Critical Element Model, Critical Volume Model, Parallel architecture Model. For additional information regarding early application of biological modeling in treatment planning, the reader is referred to a review by Orton.et al. In this study, the LKB model has been used for NTCP Calculation [5].
The basic radiobiology in the mid of the last century has led to the formulation of first models of the cell kill in, eventually, to models that linked radiation sensitivity to cure rates for tumors .one of the first such formalisms was proposed by munro and gilbert [6].
Method
The study had been followed AAPM Report no -166, the modern technology the radiation oncology, Basic Clinical Radiobiology, The Basic Science of Oncology, Comprehensive Biomedical Physics, Radiation Biology of Medical Imaging, Radiobiology for the Radiobiologists, 25 project paper, many national and international journals book references, internet and my practical work was done in that department.
Radiobiology model
Dose response model divided into four types- LinearQuadratic Model, Generalized Equivalent Uniform Dose, TCP Models, NTCP Models.
Liner Quadratic model
The LQ formalism is most commonly used to model cell survival. A cell survival curve describes the relationship between the surviving fractions of cells. Radiation induced reproductive cell death has been conclusively linked to DNA damage, specifically to DNA double-strand breaks (DSB). The LQ model was introduced to relations for different fractionation regimes. The formula for cell survival is:
Generalized Equivalent Uniform Dose: The concept of gEUD proposed by Niemierko (Niemierk1997) provides a single metric for reporting non-uniform tumor dose distributions. It is defined as the uniform dose that, if delivered over the same number of fractions as the nonuniform dose distribution of interest, yields the same radiobiological effect. This equation:
Tumor control probability
A majority of mechanistic TCP models are based on the assumption that the number of surviving clonogenic tumor cells, i.e., cells capable of regrowing the tumor, follows the Poisson distribution. The Poisson assumption has limitations when clonogen repopulation occurs during treatment. One obvious problem is that simple application of exponential tumor growth predicts that all tumors recur at sufficiently long times after external beam treatment or for permanent implants with exponentially decaying sources.
Normal tissue complication probability
The NTCP models aim to describe the complication probability in normal tissues in terms of dose-response curves. As there is extensive evidence, that the radiation response of normal tissue depends on the amount of irradiated normal tissue the irradiated volume is included as an additional important parameter. The extent of the volume effect is dependent on the architecture of the respective tissue and several models have been proposed.
Materials
Common NTCP Models
NTCP is a function of total dose and number of fractions .The volume of organ tissue within the radiotherapy portal, Organ type: Serial and parallel. NTCP radiobiology models are sectioned in 2 main categories: Models based on microscopic response, and survival cell functioning-Relative Seriality, Critical Element, Critical Volume Model. Models based on macroscopic response of the organs-Lyman, Kutcher and Burman, Parallel architecture, Weibull distribution model.
Lyman, Kutcher and Burman
The most often used NTCP model is the LKB model. In the LKB model, the sigmoid dose–response curves for normal tissue complications are represented by the error function, that is, the integral of the standard normal distribution. The LKB model to account the probability of risk in normal tissue induced by radiation. TD50,m,n,Deff four-parameter model was proposed by Lyman (Lyman 1985). NTCP is calculated using the following equations,
Critical Element
The critical element model assumes that an organ consists of a number of identical functional subunits, each of them responding independently to radiation. The term “critical element” means that it is additionally assumed that a complication occurs, if a single FSU is inactivated. The critical element model is expected to describe the radiation response for organs such as spinal cord, brain or bowel. A two parameters model.
The expression for NTCP if as follows:
Critical Volume Model
The critical volume model describes tissues, where the FSUs of an organ are assumed to be arranged in a parallel fashion. The concept of FSUS defined structurally or functionally. NTCP is fully determined the number or fraction of surviving functional subunits composing an organ or tissue. A four parameters model. The parameters N, M and the dose-response model PFSU (D) for a single FSU. As the dose-response of a single FSU is unlikely to be measurable, it is derived by basic statistical and biological considerations. A four parameters model.
Parallel architecture
The Parallel Architecture Model is an increasing function of the number of FSUs inactivated by radiation. Sigmoid dose– response function is assumed to describe the probability of damaging a subunit at a given biologically equivalent dose. Apart from the assumption that biologically equivalent doses can be calculated from a LQ formula, no connections of this probability with any underlying vascular mechanism of radiation injury or identification of the subunits involved has been attempted. A two paramenter model P1 is here an increasing function of the number of FSUs inactivated by radiation. The probability that a dose D inactivates an FSU is given by the logit expression,
Relative seriality
The relative seriality model or the s-model describes response of an organ with a mixture of serial- and parallelarranged FSUs. The relative contribution of each type of architecture is described by the parameters, which is equal to unity for a fully serial organ and zero for a fully parallel organ. NTCP is given by the following equation,
Weibull distribution model: In this model the mathematical expression for NTCP, PI is based on a modified Weibull function.
Results
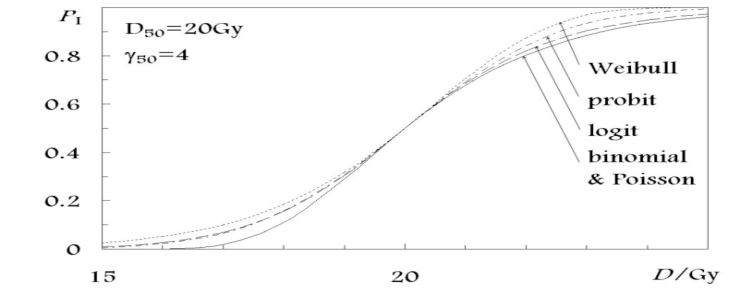
Dose-response models can be categorized into several groups based on the statistical distribution. They use for describing the sigmoid shape of the dose-response curve (Figure 2). The five distributions used in the models investigated in the present study are the poisson, binomial, probit, logit, and Weibull distributions.
Discussion
Radiobiological modeling of radiotherapy plans are used for treatment plan comparisons. Radiobiological model plays a important role in plan optimization & evaluation in radiotherapy though aim of radiobiological model is to predict the radiation response in order to achieve radiotherapy goal like Tumor Control Probability & Normal Tissue Complication Probability. The goal of radiation therapy is to deliver a therapeutic dose of radiation to target tissues while minimizing the risks of normal tissue complications. The Lyman-Kutcher-Burman model proposed by Lyman. The Lyman-Kutcher-Burman model still suitable model for treatment plan evaluation & optimization. The most of treatment planning system like Eclipse, Monaco, Ray Station used Lyman-Kutcher-Burman based NTCP model including within the LQ formalism. The suitable model of NTCP calculation in treatment planning is Lyman-Kutcher-Burman model as it predicted almost same as the other complicated model & other model can be used when absolutely necessary. The five statistical parameters which were the poisson, binomial, probit, logit, and Weibull distributions have been used to investigate the different radiobiological models for NTCP in different articles.
Conclusion
From the above discussion evident that, the 15 literature reviews, most of the works have been used to the treatment plan evaluation. The treatment plans have been compared according to the biological evaluation. This paper has been proposed overall biological evaluation tools, which give information both healthy tissue and target
volume. In this study, there is a significant radiobiological modified treatment planning has been using the biological criteria. This study shows to make out the biological evaluation and make more accessible current radiobiological modeling knowledge, and may serve as a useful aid in the prospective and retrospective analysis of radiotherapy treatment plan.
In present study, Number of Models compared with six of these NTCP Models: The Critical, the Relative Seriality model & the Critical element model the Lyman-Kutcher -Burman model, the Parallel architecture, and the Weibull distribution model. In this study, Lyman–Kutcher–Burman NTCP model has been most used in treatment plan evaluation. The common parameters γ50, M, N, D50, has been used in the treatment planning system.
3DCRT, IMRT, VMAT, and Helical Tomotherapy (HT), treatment planning system has been used to the radiobiological models. Radiotherapy planning software Philips, Pinnacle, Monaco, Eclipse, Raystation, has been used to calculate the biological responses in this study.
Still now, no standard protocol can be used for NTCP calculation due to problem of accurate NTCP model and absolute parameters. It should be more specific to maintain accurate use of published parameters values because the published data are available for many tumor sites and complication parameters in different models.
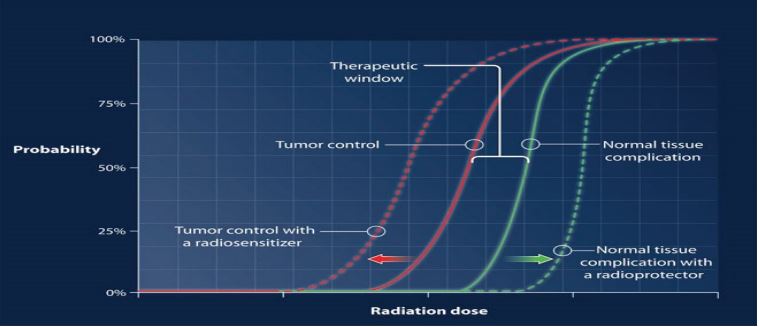
Figure 1: The normal tissue complication probability.
Figure 2:Statistical distribution used in NTCP models to describe the shape of the dose response curve. The Success of any Practical Implementation of the Concept of NTCP in Treatment Planning Depends: 1. Treatment planning & normal tissue specific parameters. 2. Extrapolate NTCP to other treatment modalities.
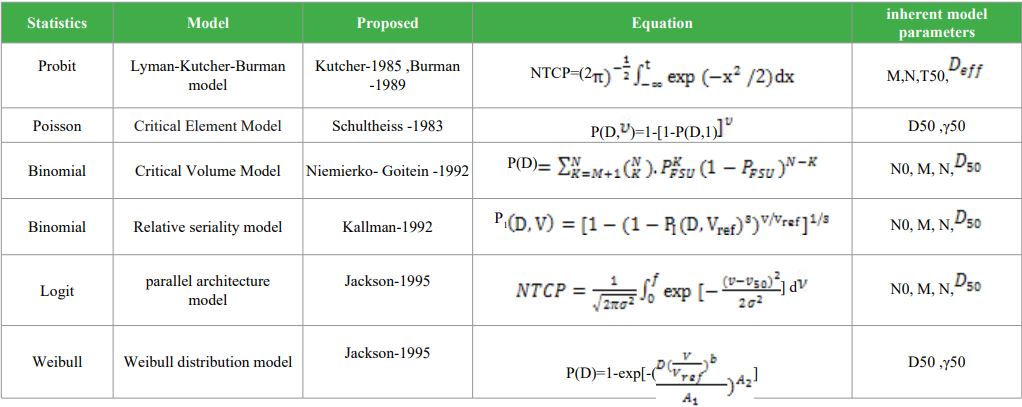
Table 1: Overview of the dose-response models together with a summary of their inherent parameters.
| Company name | Phillips Pinnacle | Varian Eclipse | CMS Monaco | RaySearch Laboratories |
|---|---|---|---|---|
| Company Product | Phillips medical system ,Andover | Varian medical system, Paloalto | Maryland Heights | Raystation |
| NTCP | Lyman-Kutcher-Burman model, Kallman S model | Lyman-Kutcher-Burman model, Kallman S model | Parallel Architecture model | Lyman-Kutcher-Burman model, Kallman S model |
Table 2: NTCP Model used in Different Treatment Planning System.
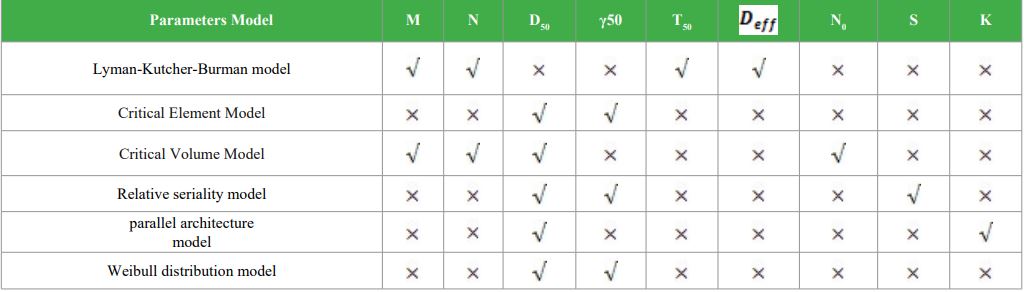
Table 3: Parameters used in Derivation of different NTCP Model.
Luxton G, Keall PJ, King CR (2008) A new formula for normal tissue complication probability (NTCP) as a function of equivalent uniform dose (EUD). Physics in Medicine and Biology 53: 23-36.[ Ref ]
American association of physicists in medicine (AAPM) Radiation Therapy Committee Task Group -166 (2012) The use and QA of biologically Related Models for treatment planning 39: 1-32.[ Ref ]
Gordon SG (2002) Dose-response relationship in radiotherapy. Basic clinical Radiotherapy. Edward Arnold, Great Britain.[ Ref ]
Niemierko A, Goitein M (1991) Calculation of normal tissue complication probability and dose-volume histogram reduction schemes for tissues with critical element architecture. Radiother Oncol 2: 166-176.[ Ref ]
Dritschilo A, Chaffey JT, Bloomer WD, Marck A (1978) The Complication probability factor: A method for selection of radiation treatment plans. British Journal of Radiology 51: 370-374.[ Ref ]
Niemierko A, Goitein M (1993) Modeling of normal tissue response to radiation: the critical volume model. Int J Radiat Oncol Biol Phys 25: 135-145. [ Ref ]
Hendry J (2014) Radiation Biology and Radiation Safety. Comprehensive Biomedical Physics. Elsevier, Oxford.[ Ref ]
Alber M, Mayo C, Niemierko A (2011) The use and QA of biologically related models for treatment planning: Short report of the TG-166 of the therapy physics committee of the AAPM. Med Phys 39: 1388-1407.[ Ref ]
Burman C, Kutcher GJ, Emami B, Goitein M (1991) Fitting of normal tissue tolerance data to an analytic function. Int J Radiat Oncol Biol Phys 21: 123-135.[ Ref ]
Joiner M, Kogel AVD (2009) Basic clinical Radiotherapy. Holder Arnold Ltd, Great Britain.[ Ref ]
Michalski A, Atyeo J, Cox J, Rinks M (2012) Inter- and intra-fraction motion during radiation therapy to the whole breast in the supine position: A systematic review. Journal of Medical Imaging and Radiation Oncology 56: 499-509.[ Ref ]
Friedland W, Kundrat P (2014) Radiation Therapy Physics and Treatment Optimization. Comprehensive Biomedical Physics. Elsevier,Sweden.[ Ref ]
Karger PC (2006) Biological Models in Treatment Planning. New Technologies in Radiation Oncology. Springer, Heidelberg.[ Ref ]
.Jackson A, Kutcher GJ, Yorke ED (1993) Probability of radiation-induced complications for normal tissues with parallel architecture subject to non-uniform radiation. Med Phys 20: 613-625.[ Ref ]